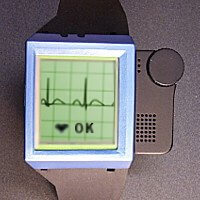
 In this article, we present a simple approach for implementing a pulse analyzer for devices with limited computational power, such as mobile and wearable computers. The main purpose of this system is to continuously monitor the ECG of a person and detect any possible heart abnormalities. The idea is to break the required computation in two parts. The learning and model building part that requires high computation is done on a desktop computer. Once the model for a person is built, it uses a low computational cost signal analysis approach to analyze the signals in real-time. The system has been implemented on an IBM WatchPad, a wearable Linux computer designed as a watch. The experiments conducted show that the system produces reliable results. This approach can benefit the embedded systems in the medical domain, such as the personal health monitoring devices, etc.
In this article, we present a simple approach for implementing a pulse analyzer for devices with limited computational power, such as mobile and wearable computers. The main purpose of this system is to continuously monitor the ECG of a person and detect any possible heart abnormalities. The idea is to break the required computation in two parts. The learning and model building part that requires high computation is done on a desktop computer. Once the model for a person is built, it uses a low computational cost signal analysis approach to analyze the signals in real-time. The system has been implemented on an IBM WatchPad, a wearable Linux computer designed as a watch. The experiments conducted show that the system produces reliable results. This approach can benefit the embedded systems in the medical domain, such as the personal health monitoring devices, etc.
Introduction
Pervasive computing has been evolving radically for the past few years and it is seen as an emerging trend of computing in the future. Mobile and wearable computers are the two areas in pervasive computing that are more obvious in our daily life and we have seen how they can make our life easier and more productive. One major area of applications for wearable computing devices is healthcare. For the patients with critical disease that requires round the clock monitoring, such as heart abnormality, wearable computing devices can monitor heartbeat and pulses, and can raise an alarm if some critical condition is diagnosed. But, quite often, these devices only have very limited computational power and storage space. This prevents them from being used for some serious computation such as pulse analysis.
The system that we have implemented takes the pulse signal from patients as input. The pulse signal that will be analyzed is input as a sequence of digital Electrocardiogram (or ECG) data sampled at a constant sampling rate. The way how the ECG signal is being sampled and digitized is beyond the scope of this article. In order to understand how the signal analysis works, we must have some basic knowledge about ECG waveform. The heartbeat of each individual consists of a distinct number of cardiological stages. Each of these stages will contribute a different set of features in the ECG waveform, due to the electrical activation by the muscle cells in particular regions of the heart. Figure 1 depicts the ECG waveform of a person with a healthy heart excerpted from [1].
The typical features of an ECG waveform are the P-wave, the QRS-complex, and the T-wave. Occasionally, a small U-wave appears after the T-wave. The cardiac cycle begins with the P-wave (marked as Pon and Poff in Figure 1), which corresponds to the period of atrial de-polarization in the heart. The most distinguish feature is the QRS-complex, which occurs during the ventricular de-polarization (from point Q to point J in Figure 1). The ventricular re-polarization that takes place after that will produce the T-wave. In the absence of U-wave, the end point of T-wave (marked as Toff) signifies the end of the cardiac cycle.
Related Work
There are vast numbers of research that related to ECG analysis in the computing science domain. They had given us much motivation and inspiration into our work. Hughes and his colleagues [1] had proposed a method to segment an ECG waveform automatically into its basic features described above. LePage [2] and his teammates had focused more on the extraction and analysis of P-wave to determine the possibility of atrial fibrillation, which refers to a heart abnormality that causes irregular heart rhythm. Both of them used wavelet transformation to analyze the ECG signal and extract its features. Although wavelet transformation is proved to be a robust system when comes to signal analysis, however, they are naturally mathematically complex and ill-suited for devices with limited computational power to produce real-time result. A stochastic hidden Markov model is used in both works for post-analysis tasks like evaluating the signal features to determine the corresponding states in the heart. Hidden Markov model has been long known as a popular tool in the speech recognition domain due to its high versatility and adaptability under different circumstances. Refer to Rabiner’s paper [3] for a comprehensive tutorial on hidden Markov model. We used hidden Markov model in our system to detect the possible heart abnormalities based on the given ECG.
Signal Analysis and Feature Extraction
As we mentioned earlier, we assumed that the system takes the input as a sequence of discrete digital ECG wave samples at a constant sampling rate. In a simpler term, the input is merely a stream of numbers. Therefore, the initial stage of signal analysis is to examine these numbers and attempt to find their correlations that constitute to the features of our interest. Each feature is an attribute of the input signal at a particular time instance. We had identified three significant features for our case, namely Increasing, if the signal is increasing at a particular instance; Decreasing, if the signal is decreasing; and Zero if the signal is stationary, or it only exhibits a slight increase or decrease. (The tolerance of the slight increase and decrease is determined by a preset threshold.) Determining these features from the input signal is done by differentiating it at a specific time instance. However, since we are dealing with digital signal, therefore we can’t use the derivative calculation for continuous function. Thus, we had adapted the calculation for differentiating digital signal. The idea is to calculate the signal changes by averaging the signal samples around the target sample to be differentiated, which can be formally defined as,
where x is a sequence of samples from the input signal, x[i] is the i-th sample of the input signal, i is the index of the target sample to be differentiated, and d(i, x) is the measure of signal changes at ith sample. n determines the number of samples taken before and after the target sample to be averaged for the calculation. A small n value will make the computation more sensitive to slight signal changes. But this also means a minor noise in the signal will have a strong effect on d(i, x), which could possibly create an unwanted artificial feature. In contrary, a large value of n will lessen the effect of noise on d(i, x), but excess averaging across the neighboring samples can cause inaccurate computation of d(i, x). The best value of n depends on the nature of the signal to be processed, which is best determined empirically. In our implementation, we had chosen n as 4 based on the calibration against our ECG dataset that is comprised ECG signals produced by large sample of individuals. In reality, this can be treated as manufacturers’ preset that can be fine tuned for specific individual. Note that we assumed the source ECG signal is always sampled at a fixed sampling rate. Thus, if the sampling rate is a variable in the system, the equation above must modify to take into account of the sampling interval to ensure d(i, x) produce the result in the same time unit regardless of the signal sampling rate.
To improve the tolerance of the signal analyzer to trivial noise, so that the features in the signal can be determined more reliably, multiple scale-space signal analysis is done by applying median filter of multiple window size to the signal in parallel before executing the feature extraction. Median filter is often used in digital signal processing to reduce “salt and pepper” noise while still preserving the significant details in the signal [4]. Prior to the features extraction process (as discussed above) is being performed, the original input signal (denoted as S0) is filtered by three median filters in parallel, with each of different window sizes (w=3, w=5 and w=7), to produce three new signals (S1, S2 and S3 respectively). We will refer them as signals at different scale-space with respect to the original signal. These signals are slightly different among each other, but they look similar generally, as illustrated in Figure 2. Then, the feature extraction process is carried out in the similar fashion as above by calculating (i, x) for every sample of the S0, S1, S2 and S3. The features extracted from each sample of these signals are compared against each other, and only the feature that is consistent across all scale-space is preserved, and it is known as the true feature. The pseudocode for this process is as follow,
What we are trying to do here is comparing the features of the signal at different scale-space. The intuition behind is, if a feature is the true feature of the signal (as oppose to noise), then it will not be destroyed by the median filter but should appeared in the signal of every scale-space. Of course one can argue that this approach will not work on a weak but true feature, such as abrupt signal changes, which will be most probably treated as noise and filtered out in one of the scale-space. Clearly, we have paid a small price in terms of preciseness for achieving better accuracy in extracting the feature. Even so, this tradeoff had showed an acceptable result in our implementation.
Feature Analysis and ECG Models Construction
We used the hidden Markov model to model the ECG of different heart characteristic. The hidden states are basically the major features of an ECG waveform, i.e. P-Wave, QRS-Complex, T-Wave, and Baseline, while the observable states are defined by the signal features, such as Increasing, Decreasing, and Zero. Figure 3 depicts the hidden states and one of the possible state transitions. The precise definition for each hidden states are:
- P1: The increasing portion of P-Wave
- P2: The decreasing portion of P-Wave
- Base 1: Baseline 1 (refer to Figure 1)
- Q1: The increasing portion of QRS complex.
- Q2: The decreasing portion of QRS complex.
- T1: The increasing portion of T-Wave
- T2: The decreasing portion of T-Wave
- Base 2: Baseline 2 (refer to Figure 1)
The transition arcs in Figure 3 can be safely ignored since they merely illustrate one of the possible states transition. Moreover, the states transition will be constructed automatically by Baum-Welch algorithm [3], which is an iterative algorithm for training the hidden Markov model. In a nutshell, this algorithm takes an observations sequence, which in our case is a sequence of signal features extracted from the ECG, and then the algorithm will construct (or train) a model that is optimized for the particular observations sequence (the training sequence in this case). We collected the training sequence from the ECG produced by a healthy heart, and several other types of heart abnormalities. The ECG will be segmented into intervals of complete cardiac cycle. Then, we used this algorithm to construct the ECG models of different heart characteristics. However, since we are training a model against a set multiple of training sequence, with each sequence as a series of features extracted from an ECG interval of a particular heart characteristic, and there are multiple ECG intervals that correspond to the same heart characteristic. Therefore, we had used the modified version of Baum-Welch algorithm that works for multiple independent observations sequence as proposed by Li and Parizeau [5].
After the ECG models of different heart characteristics are constructed, an unknown ECG interval from the user can be identified using the Forward algorithm [3], with the ECG model that generates the highest probability relative to the rest as the most probable match of the possible heart characteristic. To decode the underlying hidden states of a particular ECG interval, the Viterbi algorithm [3] is used instead.
Implementation and Results
The system was implemented for a IBM Linux WatchPad. It’s a low power 32-bit ARM CPU (18-74 MHz) based device. It has low-power DRAM of 8MB, and Flash memory of 16MB. The device has a 320×240 B/W LCD display, touch panel, Bluetooth (V1.1w/ voice), IrDA (V1.2), UART (Cradle), speaker, microphone, accelerometer, vibrator and RS232C. It runs Linux Kernel 2.4.18, IBM BlueDraker and X-windows X11R6.
For the sake of modularity and ease of testing, we implemented the signal analyzer as a separate executable program with the hidden Markov model used for feature analysis. Both of them are piped together using the standard process piping by connecting the standard output of the signal analyzer to the standard input of the feature analyzer. In our prototype, the source ECG data is streamed from an external file to the signal analyzer’s standard input for simulating a continuous ECG reading from the user. The output result is produced by the feature analyzer through the standard output to inform the user of the possible heart abnormalities based on the ECG reading. In the later stage, we also managed to display the ECG waveform being analyzed graphically when we tested it on the X Windows system running on IBM WatchPad. A major challenge when transforming the concept of the two modules into implementation is, due to the streaming input data source, therefore we had to buffer the data until they are sufficient to be analyzed correctly. This might not be as straightforward as it seems to be, especially when the streamed data is filtered in parallel by three median filters of different window size. We must ensure that the output is available from all filters before proceeding to the subsequent processing pipeline.
A serious problem that had bothered us for quite some time in our hidden Markov model implementation was investigating why the training algorithm does not produce an optimum model based on the given observations sequence. When we had just implemented the hidden Markov model, we tested its three major algorithms (namely Forward algorithm, Viterbi algorithm, and Baum-Welch algorithm) against some test data found on some websites. We were very happy since the result conforms to the expected output. But when we trained the model against our ECG data, it does not produce an optimum model, i.e. when we run the Forward algorithm against the same training sequence, we get a very low (near-zero) probability, which we believed it is wrong. We thought that maybe the iterative algorithm was caught in the local maximum (as it might be). More surprisingly, the training process terminates so quickly, which is way faster than we expected for such a long training sequence. This had given us a hint on the problem. It turned out that the iterative algorithm often terminate in the second iteration. Since both iterations produced a very low probability that beyond the precision of a 64-bit floating point. There was nothing wrong with the low probability as it was due to the long training sequence. However, when the difference of the two iterations result was calculated, it was very small and interpreted as “very little improvement”. Thus the iteration was terminated. The remedy for this problem is taking the log-scale of the probability when calculating the difference. Similar to when an unknown ECG is being checked, the log-scale of the probability is taken to compare the probability ratio between models.
We had tested our implementation prototype against a set of 50 labeled ECG data. Each of them is segmented into an interval that contains only a single cardiac cycle that begins with the P-Wave. They were also preprocessed to have unit energy in order to normalize the dynamic signal range and stabilize the baseline. The prototype is running on IBM WatchPad (32-bit CPU at 75 Mhz). The result was computed almost instantaneously, and exhibits an accuracy of almost 90% to detect the heart abnormality correctly from the ECG, as depicted in Table 1. The ECG models for different heart characteristic were trained on an ordinary desktop personal computer beforehand, and then they were stored on the device built-in Flash memory.
Conclusion and Future Work
We had showed a simple algorithm for analyzing a person’s pulse by examining his/her ECG reading. The algorithm exhibited a very low computational complexity and it can be used for any real-time application that running on a machine with limited processing power. Although the training process of the ECG models required a considerably amount time, it is only needed to do once, and it is usually performed on a personal computer. The storage required to keep those are models are very small that every mobile computers and embedded system can afford.
However, there is still a lot of room for further improvements. As we touched bit earlier, it would be better if the signal analyzer and feature extractor is able to work with ECG signal at different sampling rate, or in another words, the sampling rate is a variable in the system. This implies that every process in the system must take the time unit into concern in its algorithm. The challenging part will be building the ECG model, since if the model is trained by a training sequence of a specific sampling rate, meaning that it can only be used effectively under that particular sampling rate.
In a hidden Markov model, if the observations sequence gets particularly long, there is a big possibility that the calculations will exceed the precision range of the machine. This is due to the multiplications of a large number of terms with each term has the range from zero to one. If precision overflow occurs, the result produced is unreliable and unexpected error might occur. Therefore, scaling is necessary for the algorithms in the hidden Markov. Rabiner [3] covered a great deal of details into this aspect in his paper.
Another improvement will be allowing the input to be at any arbitrary point on an ECG, without the need of a compulsory starting point, which in our case, the ECG to be analyzed must always begins with the P-Wave. It would be better as well, if we don’t need to segment the ECG into their cardiac cycle intervals manually for analysis. But instead the system can take the input as a lengthy streaming ECG data, segment them automatically, and perform the analysis and checking. If this can be done, there is a high possibility that we can even show the pulse rate information to the user as well.
There are a few open questions that struck our mind as we were moving along the way. Is using hidden Markov model an ideal solution to solve the problem statement of our system? Is it really a good idea to build the ECG models of different heart characteristics for detecting heart abnormalities? What if there is an ECG from a patient that suffers a rare heart abnormality and we don’t have the particular model registered in our system, what report will the system give to the user? Can we generalize the ECG models into merely normal and abnormal?
References
- N. Hughes, L. Tarassenko and S.J. Roberts, “Markov Models for Automated ECG Interval Analysis”, Neural Information Systems Conference, 2003.
- R. Lepage, J. Bouncher, J. Blanc, and J. Cornilly, “ECG Segmentation and P-Wave Feature Extraction: Application to Patients Prone To Atrial Fibrillation”, 23rd Annual International Conference of the IEEE Medicine and Biology Society, October 2001.
- Rabiner, “A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition”, Morgan Kaufmann Publishers Inc., 1990.
- J. Stein, “Digital Signal Processing: A Computer Science Perspective”, Wiley-Interscience, September 2000.
- X. Li and M. Parizeau, “Training Hidden Markov Models with Multiple Observations – A Combinatorial Method”, IEEE Trans. on Pattern Analysis and Machine Intelligence, April 2000.


